Fun with kinetic energy: the lethality of thrown stones
In the aftermath of the death of Bassam Ibrahim Abu Rahmah, Israel supporting blogs and threads are full of claims that stones thrown by Palestinians (even though it appears no stones were thrown here anyway) can be lethal. This post serves to elucidate why this is unlikely by means of some elementary physics. All throughout I'll asssume (somewhat unrealistically) that there is no loss of energy due to air or wind resistance ('drag').
Other, more persistent Hasbarists like to make their argument even more disingenuous by adding that 'stones thrown from vantage points are even worse' (as if Palestinian demonstrators are ever allowed to take up such vantage points). For that reason I'll treat the general case of a manually launched projectile, launched from a vantage point (i.e. a point somewhat elevated with respect to the position of the target). I'll assume the vantage point to be higher than the target by h (m).
First some basics. An Olympian javelin thrower reaches typically an initial (at launch) javelin velocity of 30 m/s, with an 800 g (0.8 kg) javelin and of course the typical run-up to the throw. He transfers about 400 J(oules) of kinetic energy to the javelin. These are of course the very best ‘throwers’ in the entire world.
1. Speed of the projectile without vantage height:
This can be calculated as follows: the Kinetic Energy Ek of a moving body with speed (velocity) v (m/s) and mass m (kg) is:
Ek = 1/2 m v2
In the case of the javelin thrower: 1/2 x 0.8 x (30)2 = 360 J (Joules)
To estimate the launch velocity v' for heavier javelins, using the above we can deduce that the launch velocity of the heavier projectile will be v’ = v √(m/m’) with v the speed of the lighter object and √(m/m’) the square root (√) of the ratio m/m’ of the lighter mass (m) to the heavier mass (m’).
For a javelin of 1.6 kg, v’ = 30 x √(1/2) = 21.2 m/s, for a javelin of 3.2 kg, v’ = 30 x √(1/4) = 30 x 1/2 = 15 m/s, etc etc.
The launch velocity thus tails off quickly with increasing weight of the projectile, all other things being more or less equal of course.
And with decreased launch velocity comes also decreased range (easy to prove because independent of weight).
Heavier hand-thrown projectiles are thus no more lethal than lighter ones, unless used at point blank.
2. Added speed and energy of the projectile with vantage height:
The additional energy of a projectile launched from a vantage point is also easy to calculate.
Assume the vantage point is at height h (m, respective to target), then the object has added Potential Energy (Epot) equal to m x g x h, with m, mass (kg) and g = 9.81 m/s2 (gravitational acceleration due to free fall).
So Epot = m g h
This Potential Energy is converted into Kinetic Energy during fall, so that:
1/2 m vadd2 = m g h
and imparts extra speed equal to vadd = √(2 x g x h).
For javelins launched from 10 m vantage would increase speed by 14 m/s. For higher vantage points h' multiply with the height ratio of h’/h.
The total speed a projectile thrown by our Olympian would achieve is thus:
v = √(720/m) + √(2 g h)
or approximated: v = √(720/m) + √(20 h) (m/s)
And the total Kinetic Energy at impact:
Ek = 360 + m g h (J)
A small side note needs to be made here. It can be proved easily (but that's outside the scope of this post) that whether the thrower launches the projectile up in the air, somewhat downwards of even vertically at the target, these conclusions remain entirely valid. The type of throw will of course affect that angle of incidence at which the target is hit but not the speed or total energy.
Readers unfamiliar with the Physics concept of Work will nonetheless intuitively understand that energy of a projectile and its lethality are closely linked, with higher energy projectiles being more lethal than lower energy ones.
Let's take a fairly large rock, of say 2 kg, thrown from a vantage point of 10 m and thrown by an Olympian javelin thrower. This projectile would reach a speed of 33 m/s and a total energy of 560 J.
Let's put that into perspective: that kind of energy could be delivered (as heat) by a 7 kW (7,000 W or 7,000 J/s) commercial microwave oven in about 560 J/7,000 J/s = 0.08 seconds!
Alternatively, if we converted that energy into heat to make a cup of coffee (by heating water from room temperature to 100 DC), we'd make a hot drink... of less than 2 ml (make mine an espresso!)
Still believe manually thrown, unassisted rocks or stones are lethal weapons? Ask yourself why armies around the world don't go around throwing rocks at each other any more. So until Hamas develops the Rocket Propelled Smart Rock the AOF is fairly safe at Palestinian demos...
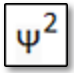

0 Comments:
Post a Comment
<< Home